Feature Detection

Characteristics of good features

What is a good feature?

• Repeatability
  • The same feature can be found in several images despite geometric and photometric transformations
• Saliency
  • Each feature is distinctive.
• Compactness and Efficiency
  • Many fewer features than image pixels
• Locality
  • A feature occupies a relatively small area of the image; robust to clutter and occlusion.

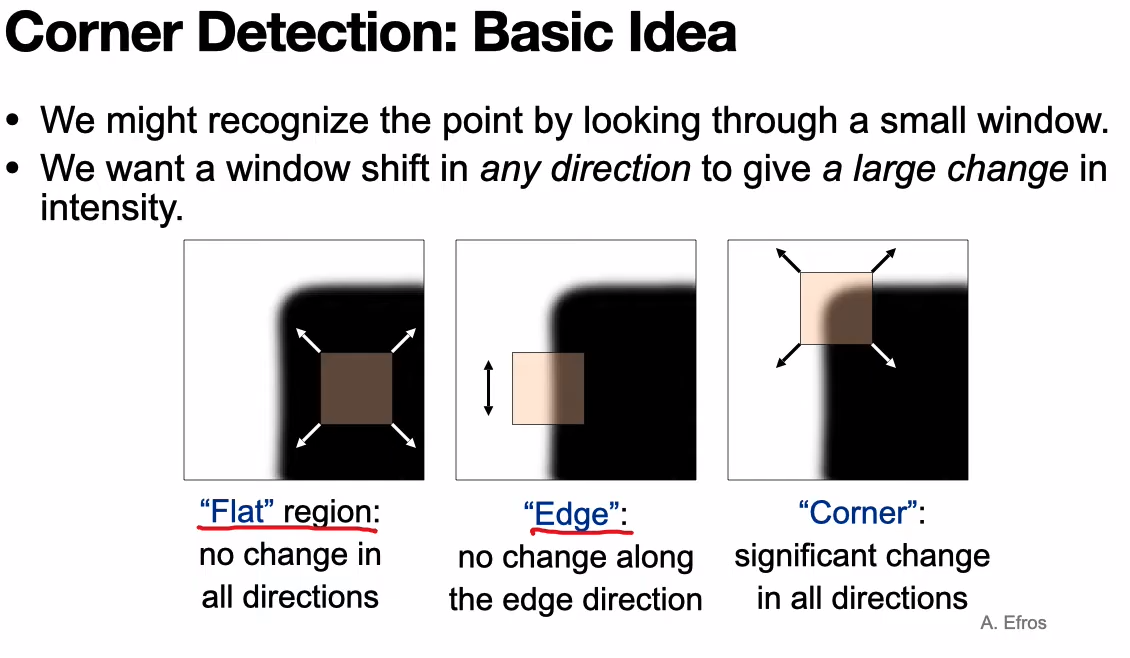
Figure1. Auto-correlation

Corner is good as a feature

• There is no change in a flat area, i.e., cloud
• There is no vertical/horizontal change in a edge, i.e., vertical/horizontal line

Therefore, we have to find out corner of image.

What is E(u,v) formular?

\[E(u,v) = \sum_{x,y}w(x,y)[I(x+u,y+v) - I(x,y)]^2\]

Corner Detection by Auto-correlation

w(x,y) : we can call it as a filter, window and mask. i.e., gaussian filter, unit step function. I(x+u,y+v) - I(x,y): the difference between the pixel value of the original image and the pixel brightness of the image moved by u+v

Figure2. Auto-correlation

Figure3. (a) : Varied a lot of changes of pixel intensity (b): Edge (c): No change

There is a lot of computational cost:

\[O(window\_width^2 * shift\_range^2 * image\_width^2)\]

ex) \(O(11^2 * 11^2 * 600^2) = 5.2 billion\)

Can we just approximate E(u,v) locally by a quadratic surface? Yes, if we use taylor series expansion

Explanation Of Talyor expansion

• Talyor Series to quadratic differential

\[f(x,y) \approx f(a,b) + f_{x}(a,b)(x-a) + f_{y}(a,b)(y-b) + \frac{1}{2!}(f_{xx}(a,b)(x-a)^2 + f_{xy}(a,b)(x-a)(x-b)+ f_{yy}(a,b)(y-b)^2)\]

Application Of Talyor expansion

Local quadratic approximation of E(u,v) in the neighborhood of (0,0) is given by the second-order Taylor expansion:

• \[E(u,v) \approx E(0,0) + \begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix}E_{u}(0,0)\\ E_{v}(0,0) \end{bmatrix}+ \frac{1}{2}\begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix}E_{uu}(0,0) & E_{uv}(0,0)\\ E_{uv}(0,0)& E_{vv}(0,0)\end{bmatrix}\begin{bmatrix}u\\ v \end{bmatrix}\]
• \[E_{u}(u,v) = \sum_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_{x}(x+u,y+v)\]
• \[E_{uu}(u,v) = \sum_{x,y}2w(x,y)I_{x}(x+u,y+v)I_{x}(x+u,y+v) + \sum_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_{xx}(x+u,y+v)\]
• \[E_{uv}(u,v) = \sum_{x,y}2w(x,y)I_{y}(x+u,y+v)I_{x}(x+u,y+v) + \sum_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_{xy}(x+u,y+v)\]

  • Let u,v equals 0: it means \(I(x+u,y+v)-I(x,y) = 0\)

    \[E_{u}(0,0) = 0\] \[E_{v}(0,0) = 0\] \[E_{uu}(u,v) = \sum_{x,y}2w(x,y)I_{x}(x,y)I_{x}(x,y)\] \[E_{vv}(u,v) = \sum_{x,y}2w(x,y)I_{y}(x,y)I_{y}(x,y)\] \[E_{uv}(u,v) = \sum_{x,y}2w(x,y)I_{x}(x,y)I_{y}(x,y)\]

Figure4. Moment Matrix means Coefficient of Quadratic function

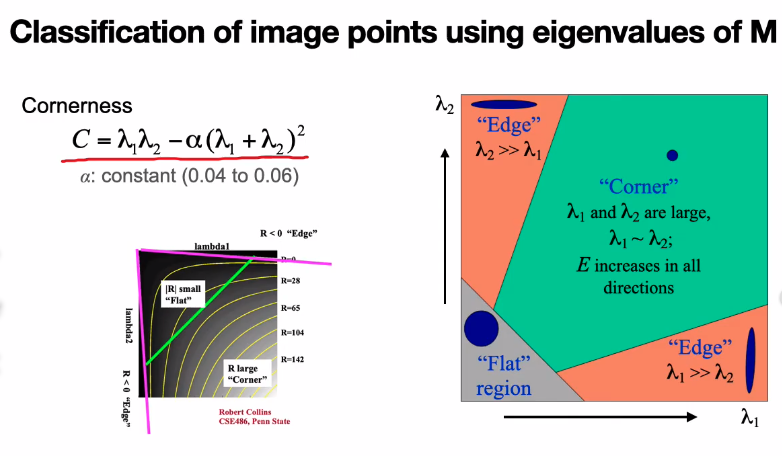
Figure5. Cornerness determines which feature is flat, edge or corner.

Figure6. Visualization of second moment matrices

Reference

• https://youtu.be/v1cdAgkCHqE
• https://www.youtube.com/watch?v=3d6DsjIBzJ4